������
�Ǝ��́uRen�@�����m�@�t�@�C���v�i�v�����g�j�ŋ����Ă��܂��B���̃t�@�C���́A�X�̒P���́q��`�r�Ɓs���_�t����₷���o�ؓ��p�ŘA�����Ă��܂��B���̃t�@�C�����g���A���k���X�̒P�������R�ɔ[���ł���悤�ȋ�������S�����Ă��܂��B
���̗�Ƃ��āA�Q�̒P�������グ�܂��B
��P�@�����ς�����������́u�h�b�v���[�����v�̍ŏ��̒P���ł��B���w�����x�̒m��������Η����ł��܂��B�ǂ�ł݂Ă��������B
��Q�@���������n�߂āA����Ɗ�����u�������x�^���v�̒P���ł��B2�̕��@�Ő������Ă��܂��B���@�T����ǂ�ʼn������B���@�U�͔��ς̏������w�K�������k����ɂ́A�������@�ł����A�w�K���Ă��Ȃ����k����ɂ͗����ł��܂���B
�@�@
��P�@�h�b�v���[���ʂ̊�{
�u�~�}�Ԃ��T�C������炵�Ȃ��瑤��ʂ�߂��čs���Ƃ��A�T�C�����̉��̍������}�ɒႭ�Ȃ�B�v����́A�T�C�����̐U�����͒ʂ�߂���O��ŕω����Ȃ��̂ɁA�ϑ��҂������U�����i���̍����j���~�}�Ԃ̒ʉߑO��ŋ}�ɕς�邱�Ƃ��Ӗ����Ă���B
��ʂɁA�q�����̐U�����Ɗϑ��҂������U�������قȂ錻�ۂ��h�b�v���[���ʁr�i��`�j�Ƃ����B
���̌��ۂ́A�}�̂悤�ɁC�x���g�R���x���[�Ń����S��S�������S��R�ւ�𑗂�Ƃ��AS���P�ʎ��ԓ�����Ƀx���g�̏�ɒu����̐���R���x���g����P�ʎ��ԓ�����ɏE����̐��Ƃ̊W�Ɠ����ł���BS���P�b����$f_S$�̂���x���g�̏�ɒu���AR���x���g�̏�̂���P�b����$f_R$�E�����̂Ƃ���BS�AR���Î~���Ă���Ƃ���$f_S��f_R$�ł��邪�AS�AR�������Ƃ���$f_S$��$f_R$�̒l�͈قȂ�B
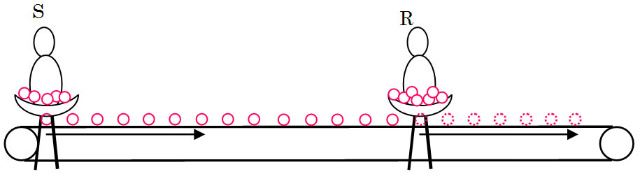
�x���g�̑�����$v$�Ƃ��āAS�AR���^�������$f_R$���ǂ̂悤�ɕς�邩���Ă݂邱�Ƃɂ���B
�i�P�jS�͐Î~���Ă��āAR��S�ɋ߂Â������ɑ���$r$�œ����Ƃ�

S�̑O���x���g��1�b����$v$[m]�����ʉ߂��邩��AS��1�b������̒���$v$[m]�̃x���g�̏��$f_S$�̊����ł���悹��BR��1�b����ɏE����$f_R$�͎����̑O��ʂ肷����x���g�ɏ���Ă����ł���B�����Ă���R�ɑ��Ă�1�b�Ԃɒ���$�iv�{r�j$[m]�̃x���g���ʂ肷���邩��A���ꂾ���̒����̃x���g�ɏ���Ă�����$f_R$���E�����ƂɂȂ�B�]���Ď��̔�Ꭾ�����藧�B
\[ v �Ff_S��v�{r �Ff_R \] \[ ���@f_R��(�@�@�@�@�@�@�@�@)f_S \]
�i�Q�j����R���Î~���Ă��āAS������$s$��R�ɋ߂Â��Ƃ��B
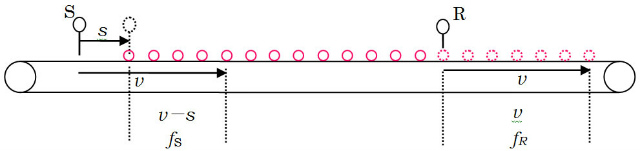
��}�̂悤�ɂȂ�A�P�b������$s$[m]�ʼn^������S�ɑ��āA�P�b�����蒷��$�iv�|s�j$[m]�̃x���g���ʉ߂���BS�͂��̒����̃x���g��$f_S$�̂��u�����ƂɂȂ�B�܂��A�Î~���Ă���R�̑O��1�b���蒷��$v$[m]�̃x���g���ʉ߂��邩��CR���E������$f_R$�Ƃ���ƁA$v�|s$�@�������$f_S$�̂��u���A$v$�̒����ɂ���$f_R$�̗ь���E������A���̔�Ꭾ�����藧�B
\[ v�|s �Ff_S��v �Ff_R \] \[ ���@f_R��(�@�@�@�@�@�@�@�@)f_S \] �i�R�jS�AR�����ɉ^�����Ă���Ƃ��A���l�ɍl�����
\[ v�|s �Ff_S��v�{r �Ff_R \]
���@�s�@�h�b�v���[���ʁ@�@ $ f_R��(�@�@�@�@�@�@�@�@)f_S $ �@�@ �t�i���_�j�@�̎����������B
�x���g�̑���������$v$�ɁCS���P�ʎ��Ԃɒu����̐��������̐U����$f_S$�ɁAR���E�������ϑ��҂̐U����$f_R$�ɂ�������u��������ƃh�b�v���[���ʂ̎��ƂȂ�B�����A�����A�ϑ��҂��^������Ƃ��A�ϑ��҂������U�����͏�̎��ŗ^������B
���̈�A�̐�������A�h�b�v���[���ʂ̒P���́A
�q�@�h�b�v���[���ʂƂ����̂́A�����̐U����$f_S$�Ɗϑ��҂������U����$f_R$���قȂ錻�ہr�ŁA���̂悤�Ȍ��ۂ́A�o�������^��������ϑ��҂��^������Ƃ��ɋN����p�A
�s $ f_R��\frac{v+r}{v�|s}f_S $ �@ �t
�ƂȂ�Ƃ������_���A���R�ȗ���Ƃ��āA�[���ł���ł��傤�B
���̂悤�ɁA�q��`�r�Ɓs���_�t�Ɓo�ؓ��p��厖�ɂ��A���k���[���ł���悤�ɋ�����悤�S�|���Ă��܂��B
��Q�@�������x�^���̌���
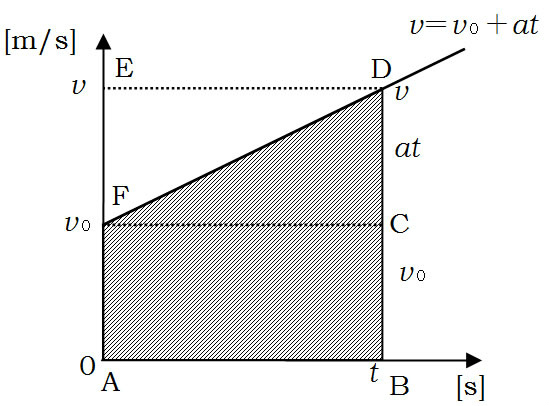
�u���炩�ȎΖʏ�����藎����S���́A���̑��x�����̊����i�����x���j�ő��������Ă���B�v�q���̂悤�ɁA�����x�����̉^�������x�^���Ƃ����B�r�i�������x�^���̒�`�j���@1�@���ȏ���4���{1��
���̕��@�́A���ȏ��̐����ɏ��������lj����Ă��܂��B���ȏ��ł́A�ȉ��̂悤�ȓ������x�^���̂S�̌����@�`�C���o���Ă��āA����Ŋ����ł��B
$v��v_0�{at$ �E�E�o$x$���Ȃ��p�E�E�@
$x��\frac{v_0+v}{2}t$ �E�E�o$a$���Ȃ��p�i$v�|t$�O���t�̑�`�̖ʐρj�E�E�A
$x��v_0t�{\frac{1}{2}at^2$�E�E�o$v$���Ȃ��p�E�E�B
$v^2�|v_0^2��2ax$�E�E�o$t$���Ȃ��p�E�E�C
Ren�����m�ł́A����ɁA1�̎��A
$x��vt�|\frac{1}{2}at^2$�E�E�o$v_0$���Ȃ��p�E�E�D
��lj����A
�s�@����D���t
���i���_�j�Ƃ��Ă��܂��B
�������R�̂P�ڂ́A
���̂T�̎��̂�������A�T�̕����ʁA�ʒu$x$�A����$t$�A�����x$v_0$�A��̑��x$v$�A�����x$a$�̂����̂P�������̂ł��B���������āA�P�̕��̂����̓������x�^���̖��Ȃ�A�A���������𗧂ĂȂ��Ă��A�ǂꂩ�̎������ʼn����Ă��܂��̂ł��B
�������R�̂Q�ڂ́A
�������x�^���̌����́A�T�̕����ʂ̂ǂꂩ�P���Ȃ��T�̎��őS�ĂȂ̂ł��B�������x�^�����w�K����ƁA������������ł�����悤�Ȋ������A����P�����Ǝv�����k������̂ŁA�T�̎��ŏI��肾�Ǝv���ƈ��S�ł���Ƃ����킯�ł��B����ɁA�T�̎��̒��œƗ����Ă���̂́A�Q�Ȃ̂ł��B�Ⴆ�A�@���ƇA������$v$�������ƁA�B�����ł�̂ł��B�������A$t$�������·C�����A$v_0$�������·D�����ł�̂ł��B���������āA�ǂꂩ�Q�̎��������L�����Ă���A�A���������Ŗ����������Ƃ��ł���Ƃ������M�������Ƃ��ł��܂��B�����o���Ă����܂��B
���@�d�Ԃ��A���鑬���ő��s���Ă��āA�u���[�L�������A�����x�|0.5$m/s^2$�ŁA400m�i��Ŏ~�܂����B�u���[�L�������Ă���~�܂�܂łɉ��b�����������B
���̂P�@�قƂ�ǂ̐��k����͇D�����L�����Ă��Ȃ��̂ŁA�Q�̎��̘A���������ʼn������ƂɂȂ�܂��B�@�ƇA�����g���Ă݂܂��B
�d�Ԃ͎~�܂�̂ŁA$v��0$������A
\[ 0��v_0�|0.5t \] \[ 400��\frac{v_0+0}{2}t \]
����2������A$v_0$��������$t$�����߂�ƁA$t��40s$
���̂Q�@�D�����g���B
$400��0�~t�|\frac{1}{2}(�|0.5)t^2$�@�@�ˁ@$t��40s$
���@2�@�K�����I�{����
���̕��@�́A���ς̏����𗘗p���Ă��܂��B�u�S�����Ζʂ�����Ƃ��̉^���́A�g�b�v�y�[�W�������悤�ɁA�}�̂悤�ɂȂ��Ă��܂��B�v
�_A���犊�藎�Ƃ��Ƃ��B
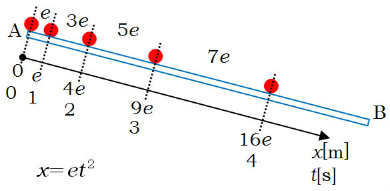
�ŏ���1�b�ԂŊ�����������$e$[m]�Ƃ���ƁA����1�b�Ԃł́A3$e$ [m]�A���̎���1�b�Ԃł́A5$e$ [m]�A���̎���1�b�Ԃł́A7$e$[m]�A�E�E�E�E�E�ƂȂ��Ă��܂��B1�b�ԂŐi�ފԊu������傫���Ȃ�A���̊����́A�P�F�R�F�T�F�V�F�E�E�E�ƂȂ�̂ł��B
�����ŁA�}�̓_A�����_�Ƃ��āA�Ζʂɉ�����$x$�����Ƃ�A�ʒu$x$�Ǝ���$t$�̊W�����߂�ƁA1�b�̂Ƃ��� $e$[m]�A2�b�̂Ƃ��� $e�{3e��4e$�@[m]�A3�b�̂Ƃ��� $4e�{5e��9e$�@[m]�A4�b�̂Ƃ��� $9e�{7e��16e$�@[m]�ƂȂ��Ă��邩��A$x$��$t$�̊W�́A
$x��et^2$�@�ƂȂ�܂��B
���x$v$�̒�`�́A$v��\frac{x'�|x}{t'�|t}��\frac{\Delta x}{\Delta t}��\frac{dx}{dt}$�@������A$x$��$t$�Ŕ������āA$v$��$t$�̊W�́A
$v��\frac{d}{dt}(et^2)��2et$�@�ƂȂ�܂��B
�����x$a$�̒�`�́A$a��\frac{v'�|v}{t'�|t}��\frac{\Delta v}{\Delta t}��\frac{dv}{dt}$�@������A$v$��$t$�Ŕ������āA�����x$a$�́A
$a��\frac{d}{dt}(2et)��2e$�@�ƂȂ�܂��B
$e$�̑���ɁA�����x$a$��p���āA$x$�A$v$��\���A
$x��\frac{1}{2}at^2�Av��at$�@�ƂȂ�܂��B
����ɁA�Ζʂ̓r�������_�ɑI��ŁA�����x$v_0$������ꍇ�ɁA��$v��at$���g������A���x$v$�́A
$v��at�{v_0$�@�E�E�o$x$���Ȃ��p�E�E�@�ƂȂ�܂��B
$v$��$t$�Őϕ������$x$�ƂȂ邩��A�i�ϕ��͔����̋t�j
$x��\frac{1}{2}at^2�{v_0t$�@�E�E�o$v$���Ȃ��p�E�E�B�ƂȂ�܂��B
�O�q�Ɠ��l�ɁA�@�ƇB������A$a$�������ƇA�����A$t$�������ƇC�����A$v_0$�������ƇD�����o��̂ł��B
�o�Q�l�p
�������A�����T�L������K�v�͂���܂���A�R���S�ŏ\���ł��B�����A�T�őS�Ă��Ǝv���ƈ��S�ł���͂��ł��B����ɁA���Ŏ����悤�ɁA$v�|t$�O���t���玮�A�A�B�A�D�������߂�ƁA�����̎��́A�����ɗ����ł���̂ŁA�L������̂��ȒP�ł��B
����$v�|t$�O���t�ŁA�i����$x$�͎ΐ����̖ʐςł��B
���̖ʐ�$x$�̋��ߕ��ŁA
��`ABDF�̖ʐς��狁�߂�ƇA�����ł܂��B
�l�p�`ABCF�̖ʐρ{�O�p�`FCD�̖ʐς��狁�߂�ƇB�����ł܂��B
�l�p�`ABDE�̖ʐρ|�O�p�`FDE�̖ʐς��狁�߂�ƇD�����ł܂��B